Georg Cantor

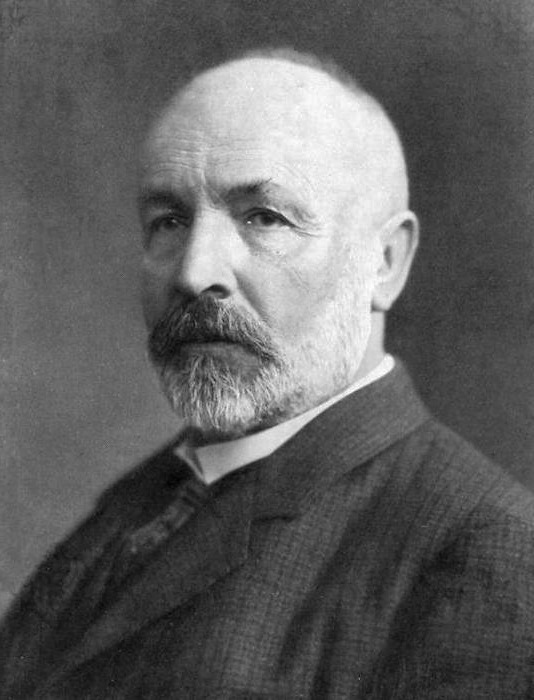Georg Cantor est un mathématicien allemand, né le à Saint-Pétersbourg (Empire russe) et mort le à Halle (Empire allemand). Il est connu pour être le créateur de la théorie des ensembles.

Il établit l'importance de la bijection entre les ensembles, définit les ensembles infinis et les ensembles bien ordonnés. Il prouva également que les nombres réels sont « plus nombreux » que les entiers naturels. En fait, le théorème de Cantor implique l'existence d'une « infinité d'infinis ». Il définit les nombres cardinaux, les nombres ordinaux et leur arithmétique. Le travail de Cantor est d'un grand intérêt philosophique (ce dont il était parfaitement conscient) et a donné lieu à maintes interprétations et à maints débats.

Cantor a été confronté à la résistance de la part des mathématiciens de son époque, en particulier Kronecker.

Poincaré, bien qu'il connût et appréciât les travaux de Cantor, avait de profondes réserves sur son maniement de l'infini en tant que totalité achevée..|groupe=n}}. Les accès de dépressions récurrents de Cantor, de 1884 à la fin de sa vie, ont été parfois attribués à l'attitude hostile de certains de ses contemporains, mais ces accès sont à présent souvent interprétés comme des manifestations d'un probable trouble bipolaire.

Au , la valeur des travaux de Cantor n'est pas discutée par la majorité des mathématiciens qui y voient un changement de paradigme, à l'exception d'une partie du courant constructiviste qui s'inscrit à la suite de Kronecker. Dans le but de contrer les détracteurs de Cantor, David Hilbert a affirmé : « Nul ne doit nous exclure du Paradis que Cantor a créé. » Informations fournies par Wikipedia